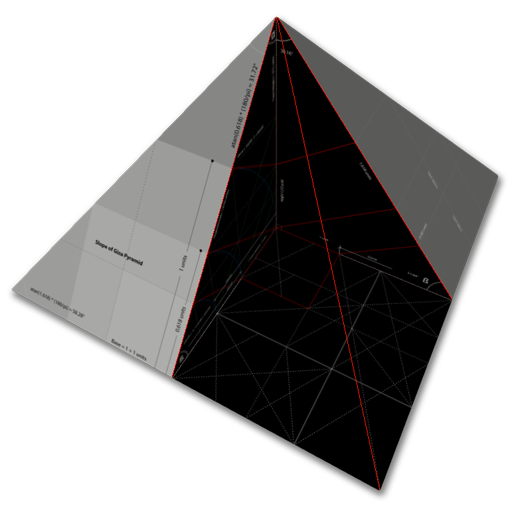
Giza Pyramiden och Rottal - Ett annat perspektiv
Observera: Detta utforskande baseras på estetisk inspiration och praktiska samt teoretiska överväganden mer än strikt matematisk noggrannhet.
Hade egyptierna kunskap om att dela ytor enligt det gyllene snittet?
För en tid sedan återbesökte jag några gamla anteckningar från 1995 där jag analyserade Giza-pyramiden med ett perspektiv baserat på rottal. Jag upptäckte snabbt att vinklarna och proportionerna var nära relaterade till "gyllene snittet" i varje vinkel och hörn. Vid den tiden kunde jag inte tro hur väl måtten stämde, så jag lade anteckningarna åt sidan. När jag tittade på dem igen insåg jag att siffrorna faktiskt stämde ganska väl.
I den här artikeln kommer jag att försöka visa dessa relationer på ett sätt som antyder att egyptierna kanske visste hur man beräknade indelningen av ytor enligt det gyllene snittet, eller mer korrekt, rottal. Jag föreslår att deras kunskap sträckte sig bortom den enkla 3:4:5-triangeln till en djupare förståelse för geometri och möjligen även trigonometri. Dessutom verkar det som att de byggde pyramiden enligt en strikt formel centrerad kring det gyllene snittet. Jag påstår inte att de använde kalkylatorer som jag gör; allt som behövs för min demonstration är pinnar och snören, eftersom det är så man kan konstruera rottal (läs mer om detta längre ner eller i min artikel "En närmare titt på rottal").
Först, låt oss titta på den välkända 3:4:5-triangeln och varför jag tror att det inte var egyptiernas enda geometriska verktyg.
 |
 |
| 3:4:5 Triangle | 1.618 Triangle |
3:4:5-triangeln är ett utmärkt verktyg för att skapa 90° vinklar. Den kan lätt förväxlas med den vända tvärsnittet av pyramiden på grund av deras likheter. Jag har omvandlat siffrorna till ett perspektiv baserat på rottal för att förtydliga jämförelsen.
I figur 2 ser vi en liknande men distinkt annan triangel. Dimensionerna på de kvadratiska formerna är inte längre trevliga, jämna, regelbundna tal. Det som fångade min uppmärksamhet är att den matchar dimensionerna på tvärsnittet av pyramiden mycket bättre än 3:4:5-triangeln.
1 * 220 = 220 (1/2 basen)
1,272 * 220 ≈ 280 (pyramidens höjd)
1,618 * 220 ≈ 356 (hypotenusan)
1,667 ≠ 1,618 (skillnaden här skulle betyda flera meter i verkligheten)
Andra har redan upptäckt det jag fann, och det har debatterats och ifrågasatts om egyptierna medvetet använde 1:0,618 / 1:1,618-formeln eller av en slump. Syftet med denna artikel är inte att bevisa något rätt eller fel, utan att presentera ett experiment för att se om det är möjligt, eller till och med troligt att pyramiden designades på detta sätt.
Jag vill också starkt betona att jag inte vill driva någon tes om att egyptierna använde dessa siffror eller nummer av någon "gudomlig", "utomjordisk intelligens" eller "kosmisk kunskaps " anledning. Jag vet inte varför siffrorna eller vinklarna stämmer så väl som de gör med min tes, men jag kommer att försöka demonstrera detta från ett perspektiv baserat på rottal.
Jag är inte matematiker, och jag tror inte att man behöver vara det för att beräkna de vinklar och relationer jag illustrerar. Rottal erbjuder det enklaste sättet att dela ytor i komponenter och relationer som är skalbara, där varje yta relaterar i proportion, area och linjedelningar till de andra elementen i samma tredimensionella form.
Låt oss börja med mätningarna. Detta är vad jag har funnit i olika litteratur och på webben:
Mått
| Höjd | 280 (146.64) , now approximately 262 (137.2) |
| Sidor | Nord 439.67(230.25) , syd 440.05 (230.25)
Öst 439.93 (230.39) , väst 439.87 (230.36) Nu ungefär 434 (227.29) |
| Hörnvinklar | Nordost 90° 3' 2" , nordväst 89° 59' 58"
Sydöst 89° 56' 27" , sydväst 90° 0' 33" |
| Orientering | Genomsnittlig avvikelse från sidorna från kardinalriktningarna 3' 6"
Basen är plan till inom 0.04 (0.021) |
Mått Approximationer
| cubits | Vad man tror |
Nuvarande | |
| Basbredd | 440 | 230.37 meter | ? |
| Höjd | 280 | 146.478 meter | 138.75 meter |
http://en.wikipedia.org/wiki/Great_Pyramid_of_Giza
Med dessa mått i åtanke relaterar hypotenusan i tvärsnittet till basbredden/2 med ett förhållande på 0,618.
Om vi förenklar siffran och sätter pyramiden basbredd till 2 enheter dyker några intressanta siffror upp. Alla som är bekanta med "det gyllene snittet" känner igen siffran 0,168. Se på detta:
sin α = (bas / 2) / hypotenusa = 220 / 356.09 ≈ 0.618
Låt oss kontrollera detta med enhetscirkeln.
I detta exempel är tvärsnittet vridet på sidan enbart för läsbarhetens skull när det ritas in i en "enhetscirkel". Enheten refererar till hypotenusan och detta är alltid 1. Med siffrorna vi känner till blir detta:
356,09 / 356,09 = 1 enhet
tan α = y / x = 220 / 280 ≈ 0,786
y = sin α = y / 1 ≈ 0,618
x = cos α = x / 1 ≈ 0,786
Vinkeln för t i grader (inte särskilt intressant i detta scenario)
t = atan(y / x) * (180/π) ≈ 38,2°
Med detta kan vi se att hypotenusan multiplicerad med y (basen) blir 1 * 0,618 = 0,618 (inte så konstigt). Men, betrakta detta (med siffrorna vi känner till):
356,09 * 0,618 ≈ 220
Det jag försöker visa är denna siffra 0,618, så ha tålamod med mig. Jag kommer att försöka förklara detta mer detaljerat senare.
Ta en titt på detta:
220 * 1,618 ≈ 356
vilket betyder
basen * 1,618 = hypotenusan
Om vi vill att basen ska vara enhetssiffran (1) kommer hypotenusan att vara 1,618, så här:
1 * 1,618 = 1,618
Detta är en förenklad tvärsnitt av Giza-pyramiden
Förklaring av formeln med Pythagoras sats:
hypotenusa = √1(unit)2 + height2
eller med de verkliga kubitvärdena (nedskalade så att 220 representerar värdet av 1):
1,618 ≈ √(220/220)2 + (280.0/220)2
Varför dessa decimaltal? De är irrationella! Egyptierna hade inte kalkylatorer som vi har. Anledningen till att jag använder siffror är för att se om geometrin stämmer. Saken är den, en kalkylator är inte ett bra verktyg för detta. Ett bättre sätt är att använda penna, papper, nålar och ett snöre. Som tidigare nämndes kan allt detta göras med pinnar och snören. Det här handlar om att arbeta med ytor (områden) snarare än raka linjer. Och det är också en av anledningarna till att proportionerna vanligtvis inte blir trevligt jämna som heltal. Rottal ger ofta irrationella tal.
0,618 Med Stolpe och Rep
Ta en titt på denna bild

Stäng av miniräknaren för en stund. Låt oss säga att vi gör en rak linje med ett snöre mellan två märken. Låt detta vara enheten 1 (den kan vara vilken längd som helst) och detta blir startpunkten för resten av layouten. Skapa sedan en rätvinklig kvadrat. Använd diagonalen för att rita en båge så att den träffar baslinjen. Den nyligen formade rektangeln har ett förhållande av 1:√2. Genom att upprepa samma procedur får vi en ny rektangel med förhållandet 1:√3 och så vidare. Tänk på detta: Du behöver inte veta någonting om Pythagoras eller någon annan sats för att kunna göra detta. Det är bara ett mycket praktiskt sätt att arbeta med ytläggningar och ytdelningar. Jag visar detta med siffror och symboler men du kan också lägga undan dessa. Det fungerar fortfarande med att använda bara pinnar och snören. Vi arbetar här med ytor (områden) snarare än siffror. Detta är hur rottal kan förstås på det enklaste sättet. Det handlar om att hantera ytor (områden) snarare än raka linjer. Och detta är också en av anledningarna till att proportionerna vanligtvis inte blir trevligt jämna som heltal. Rottal producerar ofta irrationella tal.
Om du vill lära dig mer om detta, läs artikeln "En närmare titt på rottal" och titta på detta interaktiva bevis för Pythagoras sats.
Låt oss fortsätta med samma rektangel ett tag till och se vad som händer.
Vi har använt diagonalen från rektangeln √3, skapat en √4-rektangel (samma som 1+1) och har till slut skapat en √5-rektangel.
Om du nu bättre förstår vad rotrektanglar är så ta en titt på detta:
φ = ( √5 - 1 ) / 2 ≈ 0,618
eller
φ = ( 1 + √5 ) / 2 ≈ 1,618
Intressanta siffror?
Det intressanta med detta irrationella tal 0,618 och 1,618 är att enheten 1 förhåller sig till 0,618 som 1,618 till 1. I det antika Grekland kallades detta förhållande för "phi" eller "φ". I bredare termer är detta förhållande allmänt känt som det "gyllene snittet", "gyllene ratio", "gyllene sektionen", "gyllene snittet", "gyllene talet" eller "den gudomliga proportionen".
… läs mer under sektionen "En närmare titt på 1:√5".

En närmare titt på sektionerna
Låt oss veckla ut pyramiden. Vad du ser i bilden nedan är ett tvärsnitt av Giza-pyramiden. Om du har en anständig webbläsare, det vill säga uppdaterade versioner av Firefox, Chrome eller Safari (äldre versioner av Internet Explorer fungerar inte), kan du kolla in denna interaktiva 3D-modell i WebGL, som visuellt beskriver mina teorier om Giza-pyramidens layout.
W.I.P.
Höjdprojektion
Den svarta triangeln är tvärsnittet av pyramiden och hypotenusan i den blå kvadraten är sluttningen.
1 enhet (unit) representerar 220 cubits.
Observera att detta är sluttningen, inte tvärsnittet. Enheten 1 representerar 220 kubiter.
Orginalet till denna text skrev jag på engelska 2009-12-22 och finns här:
https://www.heamedia.com/Documents/Geometry/The_Giza_Pyramid_and_Root_numbers.html
© Hans E Andersson